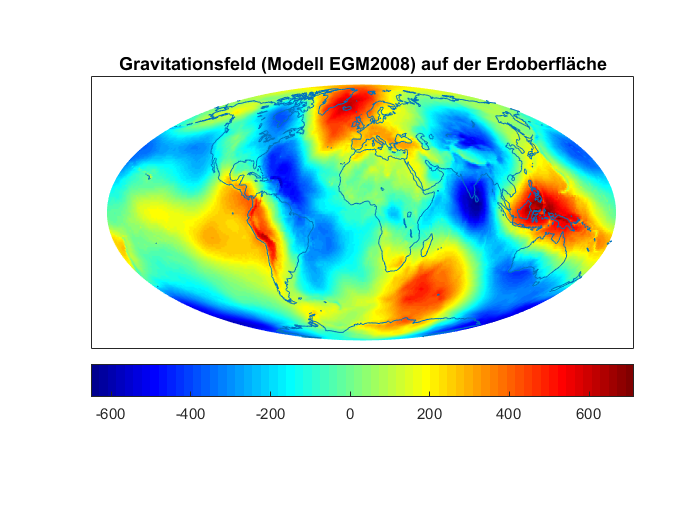
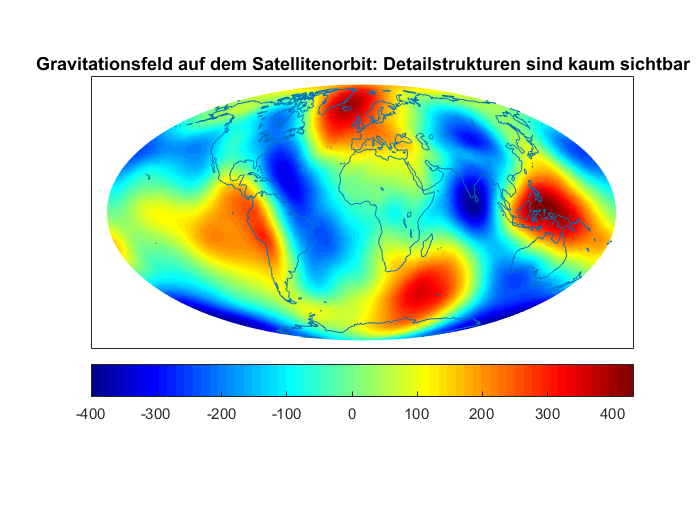
Die Erforschung der Erde geschieht im Wesentlichen durch das Lösen von einer Vielzahl von Inversen Problemen. Weite Teile unseres Planeten sind nicht zugänglich für Messungen, so dass aus der Ferne gemessen werden muss. Dies gilt für die tiefen Bereiche bis hin zum Erdkern, aber auch für große Teile der Oberfläche, wo eine flächendeckende Messung zu aufwendig wäre. Das Gravitationsfeld und das Magnetfeld etwa, zwei fundamentale Referenzen für das System Erde, werden u.a. mit Satelliten vermessen. Die so genannte Downward Continuation vom Orbit auf die Planetenoberfläche ist ein exponentiell schlecht gestelltes Inverses Problem, das heißt Messungenauigkeiten haben massiven Einfluss auf die daraus gewonnenen Modelle. Dies liegt daran, dass Detailstrukturen kaum noch messbar sind in Orbithöhe (siehe die beiden Abbildungen: Auf dem Satellitenorbit erscheint das Gravitationsfeld sehr glatt; feine regionale Strukturen, wie z.B. durch Gebirgsketten oder tektonische Grenzen, verschwinden größtenteils).
Die Ermittlung der Folgen des Klimawandels, wie z.B. das Schmelzen der Gletscher, geschieht ebenfalls dadurch, dass dessen Wirkung (Veränderung des Gravitationsfelds und damit der Satellitenbahnen) beobachtet wird und daraus (als Inverses Problem) auf die Ursache (Transport der Wassermassen auf der Erdoberfläche) geschlossen wird. Dieses Problem ist übrigens mathematisch eng verwandt mit Fragestellungen in der medizinischen Bildgebung. Es ist eine Stärke der Mathematik, durch Abstraktion solche Gemeinsamkeiten zu erkennen und dadurch neue Wege zum Lösen der Probleme zu entwickeln.
Auch die Modelle, die wir heute vom Erdinneren haben, erhält man als Lösung eines Inversen Problems: Der Aufbau der Erde in Schichten und Anomalien innerhalb der Schichten beeinflusst die Ausbreitungswege und -geschwindigkeiten von Erdbebenwellen. Aus Seismogrammen kann man daher auf die Strukturen im Inneren unseres Planeten schließen. Erneut wird also aus der Wirkung auf die Ursache geschlossen, wie es typisch für Inverse Probleme ist.
Ein weiteres Beispiel stellt die Plattentektonik dar. Hierbei entsteht das Inverse Problem nicht dadurch, dass Orte nicht für Messungen zugänglich sind, sondern theoretisch Daten zu Zeitpunkten benötigt würden, zu denen noch kein Mensch existierte. Die Vorstellung, wie die Erde vor Hunderten von Millionen Jahren ausgesehen hat, beruht darauf, dass man, wenn man die Lage der Kontinente in der Vergangenheit kennen würde, daraus die heutige Gestalt der Erde und damit verbundene Messdaten berechnen könnte. Das wesentlich schwierigere Inverse Probleme ist aber die Rückwärts-Rechnung in der Zeit: Wie konnte unser Planet beispielsweise vor 500 Millionen Jahren aussehen, wenn wir wissen, wie er heute aussieht?