In vielen industriellen Produkten spielen Faserverbundstoffe eine zunehmend große Rolle und werden dabei mit immer diverseren Anforderungsprofilen eingesetzt. Im Flugzeugbau und bei der Konstruktion von Windkraftanlagen, mittlerweile auch zunehmend beim Automobilbau, sind Faserverbundstoffe von größter Bedeutung. Diese Funktionswerkstoffe sind sehr kostenintensiv. Aus Sicherheitsgründen, aber auch aus ökonomischen Gesichtspunkten, ist eine frühe Erkennung von Defekten sehr bedeutsam, bevor größere Teile einer Struktur ausfallen.
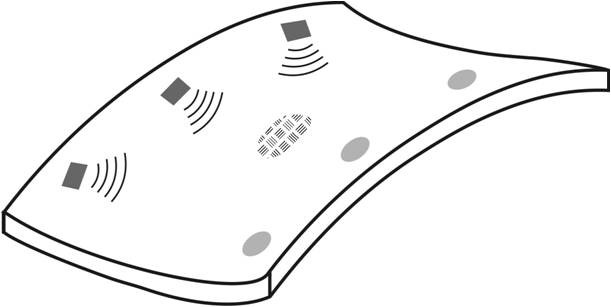
Traditionelle Materialien, wie zum Beispiel Stahl, transformieren nur langsam von einem elastischen in einen plastischen Zustand. Faserverbundwerkstoffe verhalten sich diesbezüglich anders. Kleine Delaminationen einzelner Schichten oder Haarrisse sind mit bloßem Auge kaum zu erkennen, können jedoch zu schweren Beschädigungen oder gar zum kompletten Ausfall der Struktur führen. Aus diesen Gründen sind robuste und zuverlässige Structural Health Monitoring (SHM)-Systeme sehr wichtig, um die Sicherheit zu erhöhen und gleichzeitig Inspektionsintervalle und Kosten zu reduzieren. Ein solches SHM-System besteht aus einer Anzahl piezo-keramischer Aktuatoren und Sensoren, die auf der Oberfläche einer elastischen Struktur appliziert werden (siehe Skizze unten). Die Sensoren messen dann die empfangenen Signale, die von den Aktuatoren erzeugt werden, durch die gesamte Struktur wandern und mit eventuellen Schäden interagieren.
Das mathematische Modell der Wellenausbreitung in elastischen Strukturen wird durch die Cauchysche Bewegungsgleichung beschrieben, wobei es sich, abhängig vom verwendeten Materialgesetz, um ein lineares oder nichtlineares System hyperbolischer Differentialgleichungen mit gegebenen Anfangs- und Randwerten handelt. Ein SHM-System muss dann das inverse Problem lösen, Parameter der Differentialgleichung, deren Visualisierung Hinweise auf Beschädigungen geben aus den an der Oberfläche gemessenen Sensordaten zu berechnen. Solche Parameter können zum Beispiel der E-Modul oder die Verzerrungsenergiedichte sein. Aufgrund seiner Nichtlinearität, Zeitabhängigkeit und hohen Dimension gehört dieses inverse Problem zu den anspruchsvollsten Aufgabenstellungen in diesem Bereich. Die Rekonstruktion eines Schadens basierend auf der Landweber-Methode ist in dem Bild unten zu sehen, wobei die gelben Punkte die Sensorpositionen markieren.


