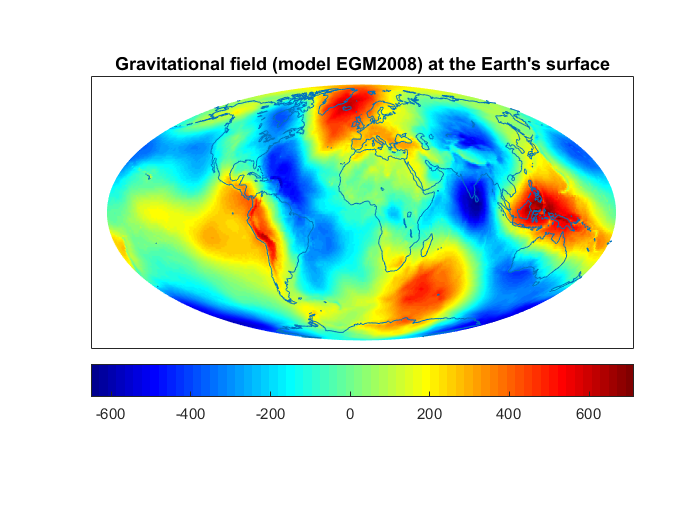
The research and exploration of the Earth is basically connected to the resolution of numerous inverse problems. Vast parts of our planet are not accessible for measurements such that only remote measurements are possible. This is the case for the deep regions up to the Earth’s core, but also for large parts of the surface, where measurements covering the whole surface would be too expensive and time-consuming.
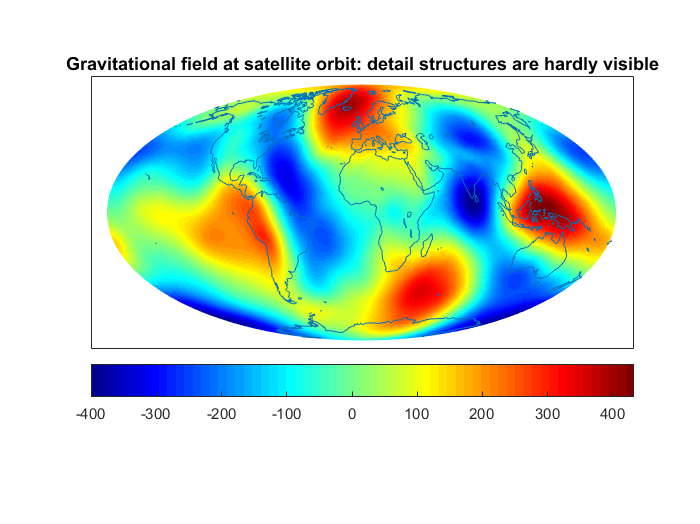
For example, the gravitational and the magnetic field, which are two fundamental reference fields for the system Earth, are measured, amongst others, by satellites. The downward continuation of the fields from the satellite orbit to the planet’s surface is an exponentially ill-posed problem. As a consequence, the contribution of noise to the measurements has an enormous impact on the gained models. The reason is that detail structures can only hardly be measured at orbit height (see the two figures: at the satellite orbit, the gravitational field appears to be very smooth; fine regional structures, e.g. due to mountain chains or tectonic boundaries, vanish largely).
The investigation of the consequences of climate change, for example the melting of glaciers, is also conducted by observing the effects (change of the gravitational field and, thus, also the satellite tracks) and concluding (as an inverse problem) on the causes (the transport of water masses at the Earth’s surface). By the way, this problem is closely related to tasks in medical imaging. It is a strength of mathematics that such similarities can be discovered by abstraction and that this can be utilized to develop new ways of solving the problems.
Also the models which we have for the Earth’s interior nowadays have been obtained as solutions of inverse problems: the composition of the Earth by layers and anomalies within the layers influences the propagation paths and velocities of seismic waves. Hence, seismograms allow conclusions on the structures in the interior of our planet. Hence, once again, we observe effects and conclude on the cause, as it is typical for inverse problems.
Another example can be found in plate tectonics. In this case, the inverse problem does not occur because measurements are impossible at some regions, but now we would theoretically need measurements at time intervals when mankind had not existed yet. Today’s images of the Earth hundreds of millions of years ago are based on the following fact: if we knew the position of the continents in the past, we would be able to calculate the shape of the Earth today and the corresponding data that would be gained today. The essentially more difficult inverse problem is the backward-calculation in time: what might have been the image of our planet, for example 500 million years ago, if we know what the Earth looks like today?
