Adaptive Optics (AO) is a technology which allows to compensate for the rapidly changing optical distortions arising during the imaging process. In ground-based telescopes, the light emitted from the astronomical objects is distorted by the turbulent nature of the atmosphere caused by, e.g., changing temperature and wind conditions. Adaptive optics is used in large scale telescope imaging (e.g., the ELT of ESO, see Fig. 1) in order to enhance the resolution of the images and to avoid costly post-processing. Equipped with the AO correction, the large ground-based telescopes are able to compete with the space telescopes with respect to the accuracy of the reconstruction.

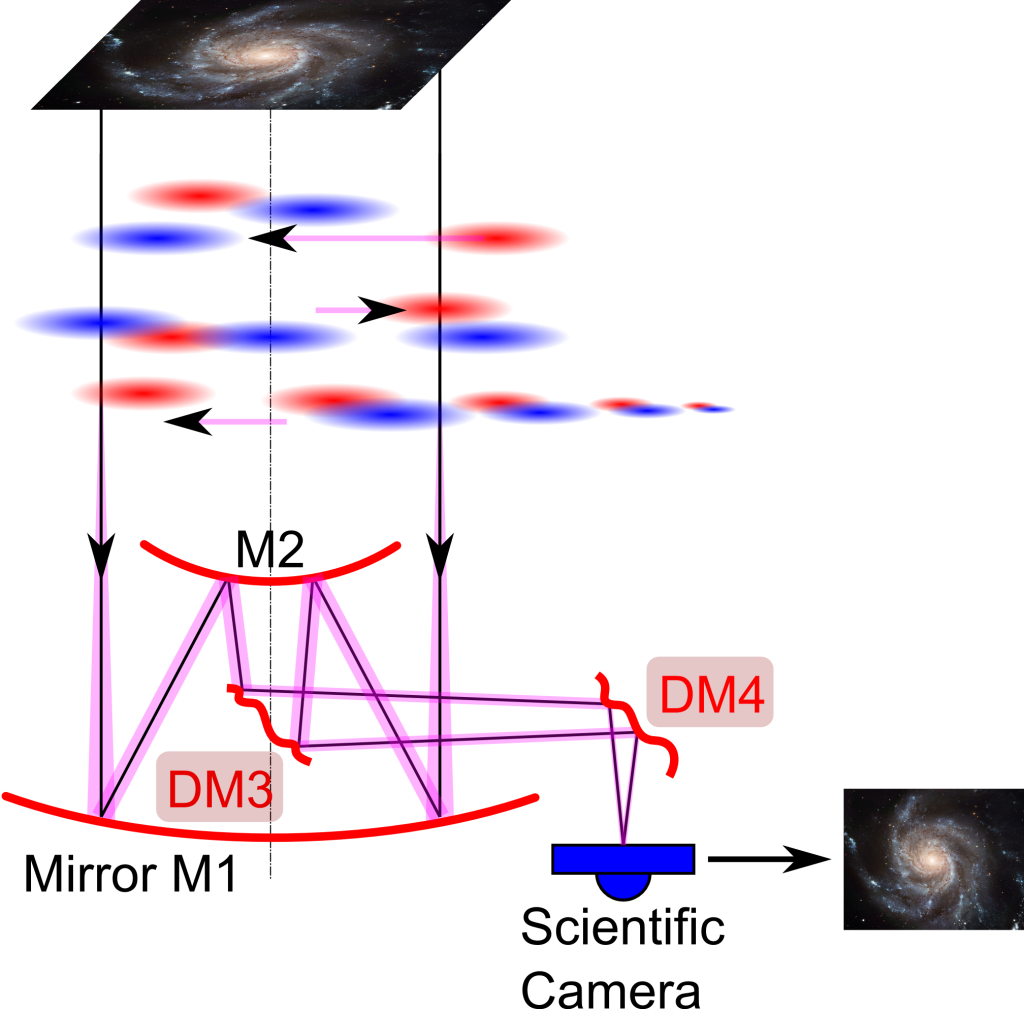
The AO mechanism is based on the measurements of the wavefront aberration and produces commands which are applied to deformable mirrors that correct the aberration, see Fig. 2. However, the correction should be fast enough, in order to keep up with the rapidly changing atmosphere. Fast computation of the corrections from a huge amount of the sensor data with acceptable quality is one challenge in the modern AO technology.
Ill-posed problems occur essentially in two steps of this process: First, reconstruction of the wave-front distortions from the sensor measurements implies reconstruction of a function from locally averaged gradients
if a Shack-Hartmann sensor ( denotes the sub-apertures) is applied. For the newer Pyramid sensors, a more complicated non-linear Hilbert-transform has to be inverted. Second, in wide-field applications the measured information about the wave-front distortions is gathered in view-directions different to the direction of the observed object. Hence, a tomography problem has to be solved, i.e., phase shifts in several atmospheric layers at hight have to be calculated from
for all guide-stars in view directions indexed by . The developed algorithms have to fulfill two major demands: First, regularization is necessary in order to avoid instabilities and too large error propagation due to the ill-posedness of the problems. Second, huge amounts of data have to be processed very fast, since the real-time requirements of the complete system are tight. In addition, all algorithms have to take evolution in time into account and allow for prediction (‘temporal control’), in order to compensate for inevitable latencies of several components.